고전 암호 (Classical Cryptosystems)
시저 암호 (Caesar Cipher)
- 평문 및 암호문 공간
- 알파벳으로 구성
- 시프트 암호 (Shift Cipher)
- 알고리즘: 평문 알파벳 별로 일정한 문자 수만큼 평행이동
- 키: 평행이동 거리 (26개)

- 전사 공격 (brute-force attack)
- 전수 조사 / 탐색 (exhaustive search)
- 0부터 25까지 각각의 키에 대해 복호화를 수행 >> 의미가 있는 평문으로 해독되는 경우 키 발견
example
해독하고자 하는 암호문: xjtzq
k=3 추정 >> ugqwn
k=5 추정 >> seoul
키는 5임을 알 수 있음
아핀 암호 (Affine Cipher)
- 시저 암호를 일반화한 암호
- 알파벳을 0~25의 숫자로 생각 (a=0, z=25)
- 알파벳 위에서 덧셈 / 곱셈 연산
- b + d = 1 + 3 = 4 = e
- d * j = 3 * 9 = 27 = 1 (mod 26) = b
- 곱셈에 대한 역원
- d와 j는 서로가 곱셈에 대한 역원
- 1/3 = 9 (mod 26), 1/9 = 3 (mod 26)
- 26과 서로소인 숫자는 모두 역원을 가짐
- 암호화 키
- 26과 서로소인 숫자 α로 가정
- 평행이동 거리 숫자 β로 가정
- 암호화 알고리즘
- 메시지 x를 아래와 같이 치환한 y를 계산
- y = α^(-1) * (y - β) (mod 26)
시저 암호 (시프트 암호) 특징
- 각 알파벳을 다른 알파벳으로 치환
- 암호화 키 = 알파벳 집합간 일대일 대응 함수
- 약점: 일대일 함수 중에서도 평행이동 함수로 한정 → 가능한 일대일 대응이 26개밖에 없음
단일 치환 암호
- 단일 치환 암호는 암호화 키로 가능한 모든 일대일 대응을 고려한 암호
- 키의 개수 = 26!
- 매우 많음
- 약 13자리 비밀번호 개수에 대응
- 알파벳 대문자 및 소문자 (52), 숫자 (10), 특수문자 (32) → 약 100개
- 그러나 여전히 안전하지 않음
- 단일 치환 암호에서 같은 문자는 항상 같은 문자로 변환
- 암호 해독은 다양한 부가정보를 이용할 수 있음
- 영어 알파벳의 출현 빈도 활용
- 영어에서 가장 자주 등장하는 단어 활용 >> the
- 의미론적 추측
다중 치환 암호 (Polyalphabetic Substitution Cipher)
- 단일 치환 암호 약점: 같은 문자는 항상 같은 문자로 변환 → 빈도 분석에 취약
- 같은 문자가 다른 문자로도 암호화되는 성질이 필요
비즈네르 암호

- 암호화 키
- 블록 크기 m: 모든 자연수가 가능
- 일대일 대응 f: = (k1, k2, ..., km)
- 블록 내 첫번째 문자는 k1만큼, 두번째 문짜는 k2만큼 shift
- 26^m 가지 키가 존재
example
m = 4, f: = (21, 4, 2, 19)
평문: "VISENERE"
| V | I | S | E | N | E | R | E |
| 21 | 4 | 2 | 19 | 21 | 4 | 2 | 19 |
| Q | M | U | X | I | I | T | X |
같은 알파벳이어도 암호화 결과가 다를 수 있음
힐 암호
- Lester Hill이 1929년에 발명
- 알파벳을 0~25의 숫자로 생각 (a=0, z=25)
- 알파벳 위에서 덧셈 / 곱셈 연산
- b + d = 1 + 3 = 4 = e
- i + x = 8 + 23 = 31 = 5 (mod 26) = e
- 4 * 6 = 24 = y
- 7 * 20 = 140 = 10 (mod 26) = k
- 비즈네르 암호에서 일대일 대응을 행렬 M 곱하기로 바꾼 것
- 암호화 키 m
- m * m 행렬 M
- 26으로 나누어 나머지를 취하는 연산에 대해 역행렬 M^-1가 존재해야 함
example
m = 2
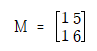
평문 JULY
- 블록 1 암호화

전치 암호
- 평문의 알파벳 순서를 재배치하는 방식으로 암호화
- A B C D E → B A D C E
- 키 : 길이 m의 문자열을 섞는 방식
- 키 공간 크기 = m! >> 일대일 대응의 개수
에니그마
- 슈르비우스(Scherbius)가 1918년에 고안
- 다중 치환 암호
- 전용 장비를 사용한 최초의 암호 시스템
에니그마 원리

- 플러그보드 (Plugboard)
- 단일 치환 암호
- 26개의 알파벳 중 n개를 골라 교차 (총 13쌍)
- 어떤 쌍을 선택하는지는 비밀 정보
- 매일 달라짐
- 회전자 (Rotors)
- 키보드에 입력 후 Right Wheel이 1/26만큼 회전
- Right Wheel 한 바퀴 회전 → Middle Wheel 1/26 회전
- Middle Wheel 한 바퀴 회전 → Left Wheel 1/26 회전
- 회전자 회전을 통해 하나의 알파벳이 여러 개의 알파벳으로 치환 가능
- 반사경 (Reflector)
- 단일 치환 암호
- 26개 알파벳 전체에 대해 교차 (13개를 골라 교차 치환)
| 날짜별 키 | 날짜별 선택 회전자 |
날짜별 회전자 결합 순서 |
날짜별 각 회전자 시작점 | Enigma 장비를 제공하는 시점에 날짜별 설정이 기록된 코드북을 사전 공유 |
| 통신 키 | 위와 동일 | 위와 동일 | 각 암호문별로 sender가 자체 설정 |
- 날짜별 키로 Sender의 시작점 키를 암호화하여 전달 - Receiver는 통신 키 암호문을 날짜별 키로 복호화하여 통신 키 복구 - 복구 통신 키로 각 암호문 복호화 수행 |
'Incognito' 카테고리의 다른 글
| Feistel Network (0) | 2022.10.22 |
|---|---|
| 일회용 패드 & 블록 암호 (0) | 2022.10.22 |
| 암호학 퀴즈 (0) | 2022.09.11 |
| RSA 암호 알고리즘 (0) | 2022.08.14 |
| [CryptoHack] ASCII (0) | 2022.08.10 |


