비트 연산
- 비트열: 0과 1로 표현된 수열 (이진수)
- 어떤 수 x가 n 비트 ↔ x는 0과 1이 n개로 이루어진 수 (01101101 → 8비트 숫자)
- 1 비트: 비트열의 최소 단위 (0 또는 1)
- 1 바이트: 8비트 비트열
- 컴퓨터는 모든 문자와 숫자를 비트열로 이해하고 처리
- 문자 / 숫자 입력 → 입력값 부호화 (encoding) → 연산 → 출력값 복호화 (decoding) → 문자 / 숫자 출력
배타적 논리합
- XOR (exclusive or): ⊕로 표시
- 비트 단위 XOR 규칙
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
- 비트열 XOR: 비트열 x ⊕ 비트열 y
- 각 비트 단위로 XOR 연산을 수행
배타적 논리합 성질
- 비트열 x, y에 대해 일반적인 덧셈의 성질을 다 가짐
- x ⊕ y = y ⊕ x (덧셈에 대한 교환법칙)
- (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) (덧셈에 대한 결합법칙)
- x ⊕ 0 = x (비트열 0이 덧셈에 대한 항등원)
- 자기 자신에 대한 ⊕는 0으로 이루어진 비트열이 된다
- 덧셈에 대한 역원이 자기 자신임
일회용 패드 (One-Time Pad)
- 버냄(vernam)이 1917년 고안
- 냉전시기 미국과 러시아 (소련) 사이 hot line을 통한 통신 암호화에 사용
- 1940년대 섀넌(Shannon)에 의해 Perfect Secrecy(완전 안전성)을 가진다는 것이 증명됨
- 암호화: 평문 비트열 p와 키 비트열 k의 XOR 연산
- c = p ⊕ k
- 키 비트열 k: 평문 비트열 p와 같은 길이 (Random 비트열)
- 복호화: XOR은 자기자신이 덧셈에 대한 역원
- c = p ⊕ k ⇒ p = c ⊕ k
Perfect Secrecy
- 어떠한 공격으로도 평문에 대한 정보를 얻는 것이 불가능
- example: apple

- 암호화 키 k는 8 x 5 비트 숫자를 random하게 선택
- 임의의 단어 p에 대하여 유일한 키 k 존재
- k = c ⊕ p
- 어떠한 단어도 같은 확률로 올바른 평문일 수 있다
- 암호문이 평문의 어떠한 정보도 포함하고 있지 않음 (암호문 자체가 그냥 random)
일회용 패드의 장단점
- 장점
- 매우 안전함
- 빠른 암호화 / 복호화 연산을 지원함 (가장 간단한 연산이 XOR만을 사용)
- 단점
- 키 배송 및 보관: 앞으로 사용할 메시지 길이만큼의 키를 사전에 공유하는 것이 필요
- 키 재사용 불가
- 키 동기화: Sender와 Receiver 사이에 동기화가 어긋날 경우 복구할 방법이 없음
- 키 생성: 대량의 예측불가능한 random을 생성하는 것이 어려움
블록 암호
- 비즈네르 암호 & 힐 암호
- 평문을 블록화
- 개별 블록에 대해 암호화
>> 이런 형태의 암호화 알고리즘 종류를 블록 암호라고 함

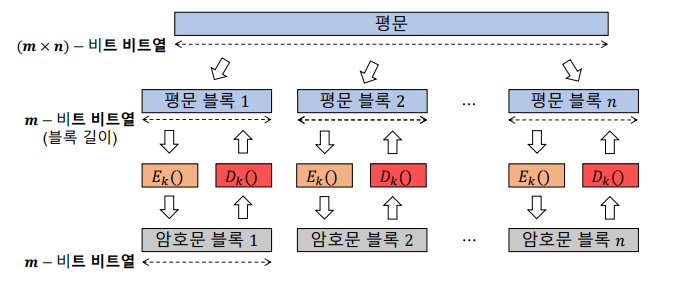
이상적인 블록 암호
- 블록 암호
- m - 비트 평문들의 집합에 대한 permutation (암호화 키)
- m - 비트 블록 집합의 크기 = 0과 1을 m개 나열하는 경우의 수 = 2^m
- {0, 1}^m에서 {0, 1}^m로 가는 permutation 전체의 개수 = 암호화 키 공간 크기 = (2^m)!
- 이상적인 블록암호는 (2^m)!개 전체에서 암호화 키를 random하게 뽑는 것
- 키를 표현하는 데 필요한 비트 수 = log2((2^m)!) > 2^m
- m = 40 → 2^40 비트가 넘는 키가 필요 (4GB) → 너무 큼
- 상용 블록 암호는 permutation 전체 집합에서 극히 일부만을 사용 (DES, AES 등)
Shannon
- 1945년, "A Mathematical Theory of Cryptography"
- 블록 암호 디자인을 위한 principle 제시
- Confusion - Diffusion Paradigm
Confusion (혼돈)
- 목적: 키와 암호문과의 관계 감추기
- 암호문의 각 자리(bit)가 키의 여러 부분(bits)들로부터 영향을 받게 함
- 키에서 1 비트만 바뀌어도 암호문의 많은 부분들이 영향을 받음

Diffusion (확산)
- 목적: 평문과 암호문과의 관계 감추기
- 평문에서 1 비트만 바뀌어도 암호문의 반 정도가 영향을 받게 함
- 암호문에서 1 비트만 바뀌어도 평문의 반 정도가 영향을 받게 함

현실한 & 안전한 블록 암호
- 블록 암호 구성 원리
- Confusion과 Diffusion의 결합으로 Round를 구성
- Round를 반복 (Iteration)
- 크게 블록 암호는 두 개의 기본 구조를 가짐
- Fiestel Network (DES의 기본 구조)
- Substitution-Permutation Network (AES의 기본 구조)
'Incognito' 카테고리의 다른 글
| AES 암호 알고리즘 (0) | 2022.10.22 |
|---|---|
| Feistel Network (0) | 2022.10.22 |
| 고전 암호 (0) | 2022.10.09 |
| 암호학 퀴즈 (0) | 2022.09.11 |
| RSA 암호 알고리즘 (0) | 2022.08.14 |


